Binary Outcomes, Risk Aversion, and Sorites Paradox (Part II)

In Binary Outcomes, Risk Aversion, and the Sorites Paradox (Part I), the main takeaway was that higher-performing agents—represented by a Binomial distribution where the probability of success is greater than 50%—might, despite better average outcomes, experience higher risk aversion due to a greater chance of negative surprises. This was visually demonstrated in Table 1, which shows how skewness in a binomial distribution shifts depending on the number of trials and the probability of success.
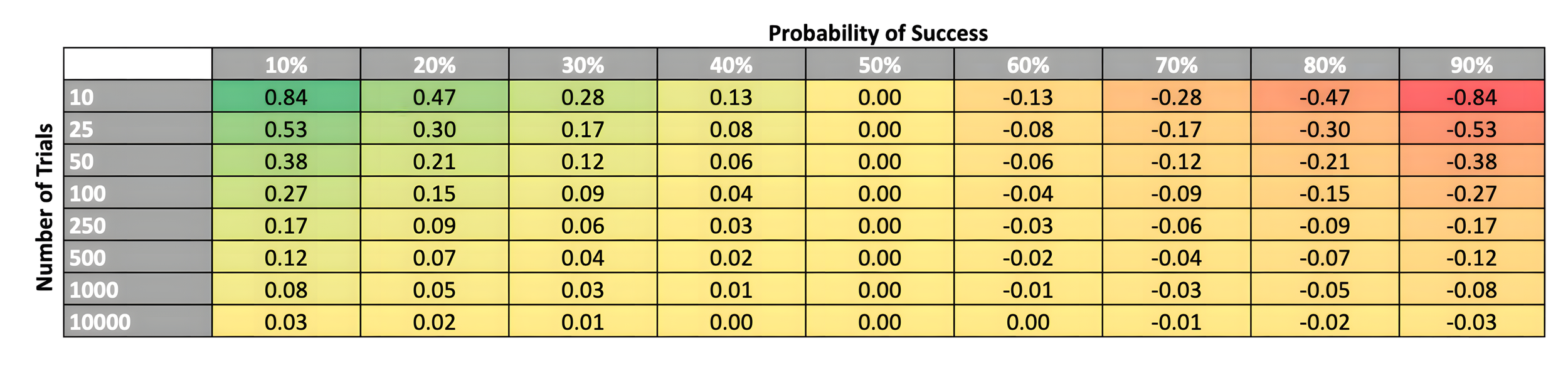
I also mentioned that it is reasonable to assume that for any given goal, we typically encounter a limited number of trials, and if successful, often end up in the top-right section of Table 1, where we observe negative skewness.
In this article, while I’ll mostly keep the assumption that we usually face a limited number of trials when working towards a goal, I’ll start by taking a closer look at the top-left part of Table 1 (after all, the other side of the table does seem a bit greener!) and then look to draw insights from distributions that do allow for number of outcomes ranging from 0 to infinity.
To explore this section, we’ll need to revisit the assumption from Part I: the idea that when starting any new task and taking the first step toward a goal, we begin with a 50% probability of success. Below, I’ve outlined some philosophical reasons why it might make sense to assume a lower probability of success at the initial stages of any experiment or task:
-
Lack of Prior Knowledge: Beginners lack knowledge about a task’s complexities, making them unaware of many factors that could lead to failure, which reduces the chances of success.
-
Skill Acquisition: According to models of learning, novices lack the procedural knowledge and intuition needed to anticipate problems, resulting in a lower likelihood of success.
-
Inductive Skepticism: Following Hume’s problem of induction, just because others succeed at a task doesn’t mean a beginner will, as each case is unpredictable and experience is needed.
We now arrive at the second key insight of this article series:
When an agent embarks on a new journey, as outlined above, it’s reasonable to assume their probability of success is less than 50%. Given this assumption, the distribution of outcomes is positively skewed!
To me, this suggests that it pays to be the “Fool”—someone who embraces the challenge of starting something new, fully aware that while the probability of success is low in the beginning, the positive skew works in their favour. This idea aligns with why the Fool is often seen as one of the most significant cards in the tarot deck. The Fool (sometimes referred to as the Joker) is rich in symbolism, representing new beginnings, spontaneity, and the thrill of adventure. Typically depicted as a carefree traveller on the verge of stepping off a cliff, the Fool embodies a leap of faith into the unknown, with innocence, openness, and a willingness to explore life without the fear of failure.
So far, we’ve explored three sections of Table 1:
-
Top-right: High probability of success, low number of trials. This resulted in high negative skew, leading to Insight 1.
-
Bottom-right: High probability of success, high number of trials. Here, we saw a low negative skew but noted that players typically won’t encounter the combination of high number of trials and high probability of success.
-
Top-left: Low probability of success, low number of trials. This produced a high positive skew, leading to Insight 2.
With that, we turn to the final part of this series and explore the bottom-left of Table 1: low probability of success and a high number of trials. In this region, we observe a low positive skew for the binomial distribution. Although we’ve stated that players typically don’t experience such a high number of trials, bear with me. I think you’ll enjoy this part, as insights from this section of the table actually lead to the development of the well-known Poisson distribution.
The Poisson distribution, defined by a single parameter lambda (λ) that is equal to distribution mean and variance, can be understood as a limiting case of the Binomial distribution when the following conditions are met:
-
The number of trials n is large (tending to infinity)
-
The probability of success p is small (tending to zero)
Note that the two conditions align with the bottom left of Table 1. An astute reader may have already noticed the key relationship that under the conditions laid outCHac above, n*p (from Binomial) = λ (from Poisson). For the more mathematically oriented, I found the derivation here to be quite clean and simple to follow. Typically, a Poisson distribution is used when one is interested in the number of rare events occurring in a fixed interval of time and space, particularly when n is large, p is small, and you know the average rate of occurrence (λ).
While it’s true that in real-world scenarios we do not encounter an infinite number of trials, we break away from our initial assumption for I believe that there’s still value in approximating the Poisson distribution as a better source of truth. The Poisson model’s assumption of infinite trials can be seen as a representation of collective wisdom—a way to capture the average outcome of countless small, independent events with low probability of success over time. Even though any individual agent or situation may only have a limited number of trials, approximating Poisson allows us to tap into this broader understanding of probability, offering insights that go beyond the constraints of a single, finite scenario. By striving to approximate the Poisson distribution, we’re effectively leveraging a more holistic model that reflects long-term patterns of rare events, making it a valuable guide even when our own circumstances are limited.
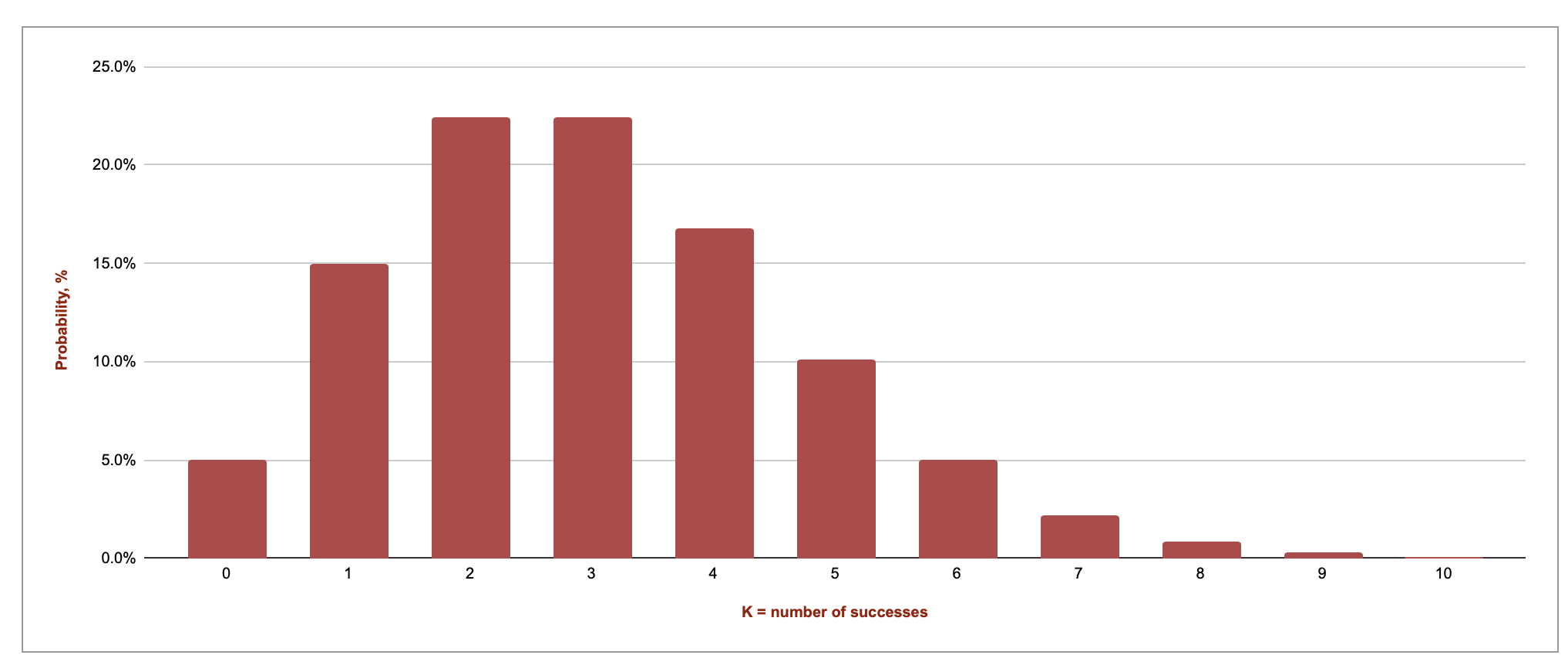
In Chart 1, I show the probability distribution for a Poisson (λ = 3). Notice how this distribution has a positive skew that aligns (relatively) well with being at the bottom left hand side of Table 1.
To further develop this connection, let’s calculate the expected probabilities of events using the Poisson distribution and compare them to the probabilities obtained when “approximating” them with a Binomial distribution.

Table 2 shows, for a constant lambda parameter (λ) = 3, the different probabilities for desired number of outcomes. Note that the highest probability for the desired outcome occurs at K = 2 and K = 3 at 22.4% with the probabilities tapering off with a positive skew. By setting up the problem appropriately, one can also quickly show that for Poisson distributions, P(X=k) = P(X=k+1) when λ = k+1.
Let’s now try and approximate P(X=3) using a Binomial Distribution. In Table 3, we vary the number of the number of trials and probability of success appropriately, with the main intention of keeping n* p = 3
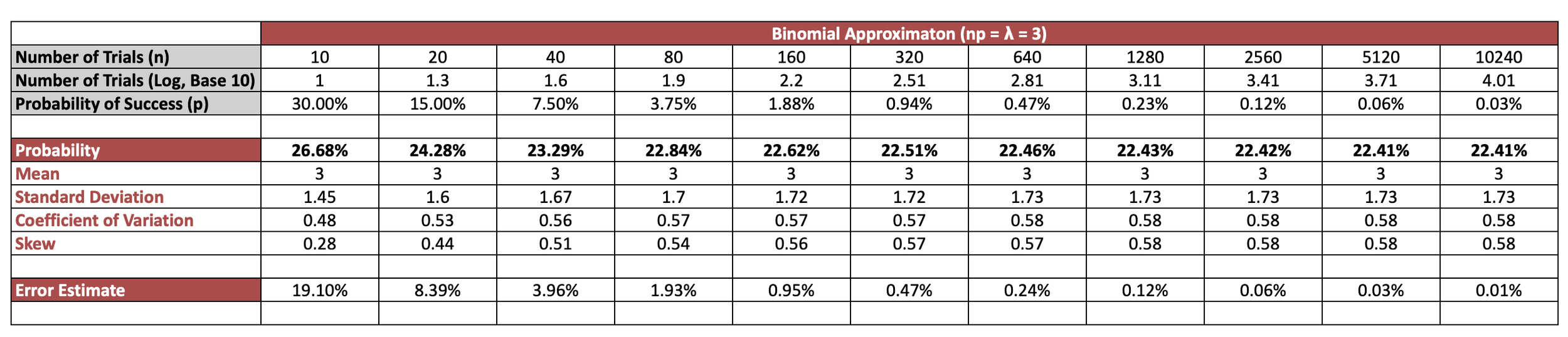
There’s a lot to unpack in Table 3. As you move toward the right-hand side, you’ll notice that the Probability, Mean, Standard Deviation, and Skew all converge toward the same values as those in the Poisson distribution with 𝜆 = 3 in Table 2. This demonstrates that as the number of trials increases, the Binomial distribution begins to closely approximate the Poisson distribution (as we’d expect to observe).
From another perspective, when the number of trials is low (and the probability of success is relatively high), the Binomial distribution tends to overestimate the probability of success.
More precisely, when using the Binomial distribution to approximate the Poisson, this overestimation is captured by the Error Estimate in the last row. As also shown in Chart 2, this error decreases as the number of trials increases, highlighting how the approximation improves as we move toward a larger 𝑛 (number of trials).
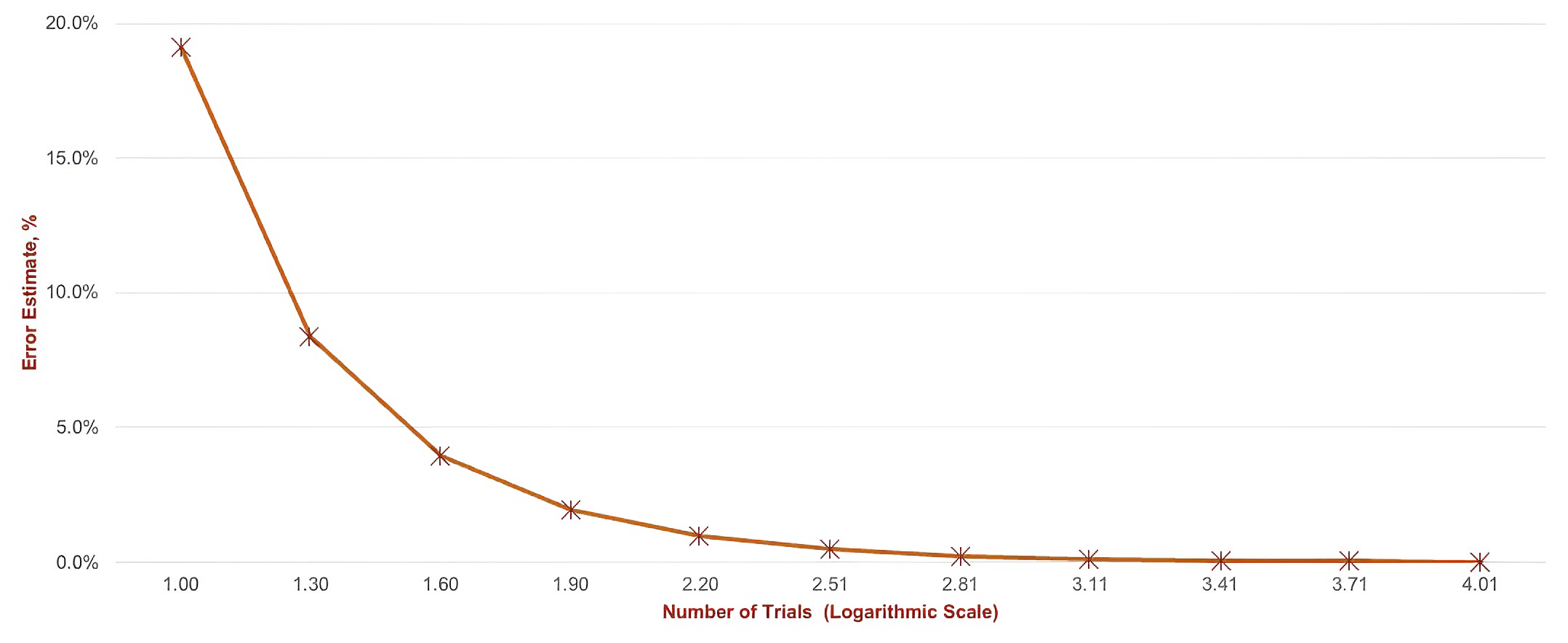
From this, we can also intuitively understand why we overestimate the probability of success when the number of trials is low. The main reason is that we’re attempting to approximate a distribution that theoretically allows for any number of events (from 0 to infinity) using a Binomial distribution, where the number of possible successes is constrained by the finite number of trials, 𝑛. In cases where 𝑛 is small, this limitation causes the Binomial distribution to overestimate the probability of success.
Interestingly, this also helps explain why skewness in the Binomial distribution increases as the number of trials grows (and corresponding probability of success decreases). As 𝑛 increases, there are more possible outcomes greater than our desired value of 𝑘 = 3, which shifts the probability distribution and increases skew.
It’s useful to examine how the error estimate changes when we try to approximate different values of 𝜆. This is captured in the sensitivity analysis below.
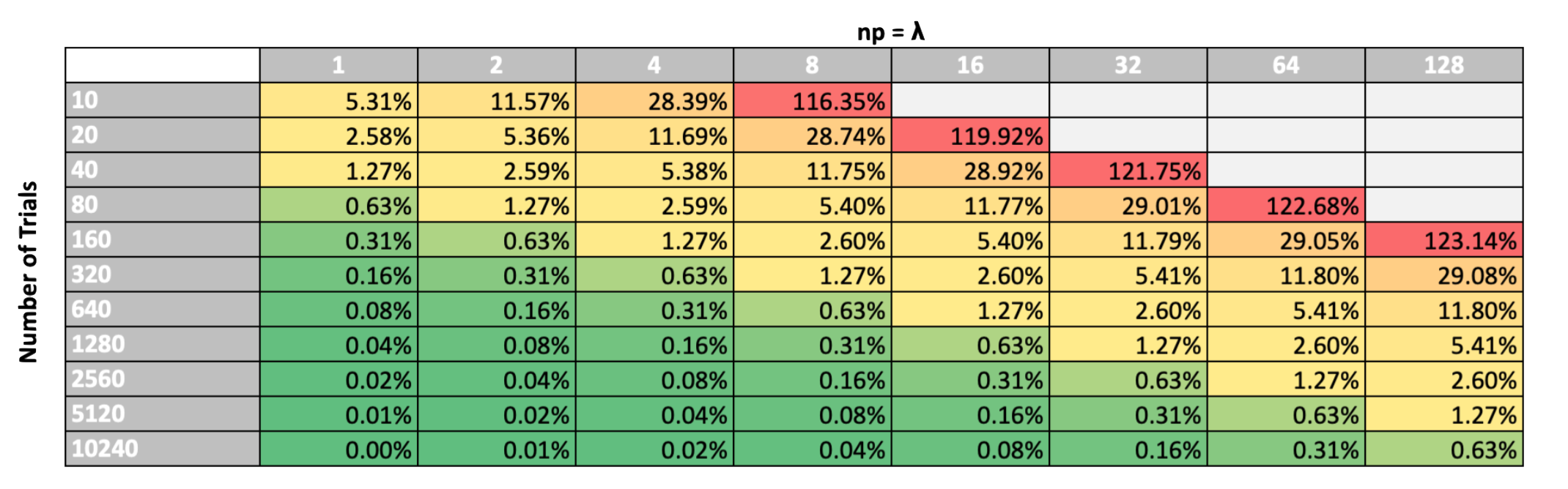
Take a look at Table 4 column by column. You’ll notice that, for a given column, the error estimate decreases by roughly 50% for an increment in m for number of trials given by: 𝑛𝑝 × 10 × m where m = 0,1,2,….. For instance, in column 2, where 𝑛𝑝 = 2, the error estimate drops from 5.36% to 2.59% as the number of trials increase from 20 to 40.
With this, we move toward the third and final insight of this article series.
The Sorites paradox is a well-known philosophical puzzle that asks: “When does a pile of sand stop being a pile if we keep removing grains one by one?” It’s challenging to pinpoint the exact moment it ceases to be a pile because the change happens so gradually.
We face a similar challenge when trying to estimate Poisson probabilities using a Binomial distribution. The Poisson distribution is often used to model rare events over time. However, the Poisson model assumes an infinite number of possible trials, which makes it difficult to apply perfectly in the real world, where events are always limited by a finite number of trials.
To address this, we approximate the Poisson distribution using the Binomial distribution. But this raises a question: When is the approximation “good enough”? Just like it’s hard to say when a pile stops being a pile, it’s difficult to determine exactly when the Binomial approximation becomes sufficiently close to the Poisson distribution.
This is where error estimates come into play. By measuring the error—the difference between the Binomial estimate and the actual Poisson probability—we gain insight into the accuracy of the approximation. As we increase the number of trials in the Binomial model, the error gradually decreases. This is akin to adding more grains of sand to the pile until it’s unmistakably a pile again.
A practical rule of thumb might be to consider the approximation “good enough” when the error falls below a certain threshold, like 5%. While we’ll never have the infinite trials that a true Poisson distribution assumes, a 5% error means that the Binomial estimate is close enough to be confidently used in real-world applications. The tolerance for this error could also reflect a player’s risk tolerance.
In this way, the error estimate acts as a guide, helping us decide when to stop worrying about the difference between the two models—much like accepting that removing a single grain of sand won’t suddenly make a pile disappear.
Conclusion
In this article series, we’ve gradually evolved our understanding of probability distributions, starting with the basic Binomial distribution and moving toward the Poisson distribution. Initially, we examined how varying the number of trials and the probability of success in the Binomial distribution can lead to different levels of skewness and risk aversion, especially when agents face uncertain outcomes. Through this, we uncovered two key insights: first, high-performing agents may experience greater risk aversion due to potential negative surprises, and second, the positive skew that arises when we lower the probability of success shows the value of being the “Fool,” willing to embrace uncertainty in the early stages of any endeavour.
We then expanded this model to include the Poisson distribution, which serves as a limiting case of the Binomial when the number of trials is large and the probability of success is small. We saw how error estimates and error thresholds (potentially another proxy for the agent’s risk appetite) provide a way to determine when the Binomial approximation is “good enough,” much like the Sorites paradox teaches us to accept gradual changes.
I hope you had fun diving into these ideas, sparring with them, agreeing, disagreeing, and everything in between. Until next time!